Solving the perfect health check rate at any scale

A few years ago, I stumbled across an interesting problem while designing a protol for master election: what is, given a number of replicas, the probability for them to start a health check that will maintain a constant probability of race condition and pressure on the lock ? In this article, we dive into this problem and find a rather elegant solution.

warning

This article leverages a homemade (or rather University made) mathematical proof, that few have reviewed. If you see an error, drop me an email.

feel free to share this article or drop a message with your feedback!

The context

In my young developer years, I had a (bad) tendency to implement lower level protocols in my apps. At that time, I did not even know about etcd and its leader election capabilities. I generally enjoyed the additional challenge and the confidence I had that no optimization was spared. This has changed over the years, but it lead me to interesting discoveries that I did not regret making. One of these is the "ideal health check rate problem", that we will discuss today.

At that time, I was designing a horizontally scalable distributed ETL for Bitcoin transactions. The existing software were not ideal, being either deprecated, unmaintained or incredibly inefficient. I therefore felt the need to make my own that would keep my databases always up to date, and the data processing pipeline concept was the following:

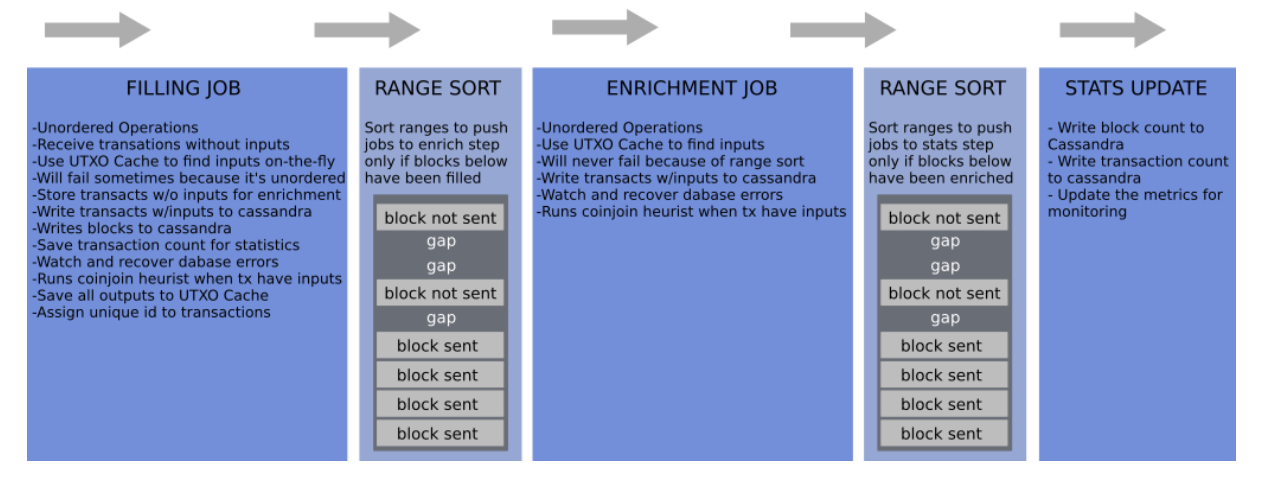
The replicas could handle any of the two types of jobs, and the jobs were passed through Redis. A master would be elected and would be in charge of the ordering steps on top of doing the jobs as all replicas do. The replicas were implementing the following protocol for health checking on each others:

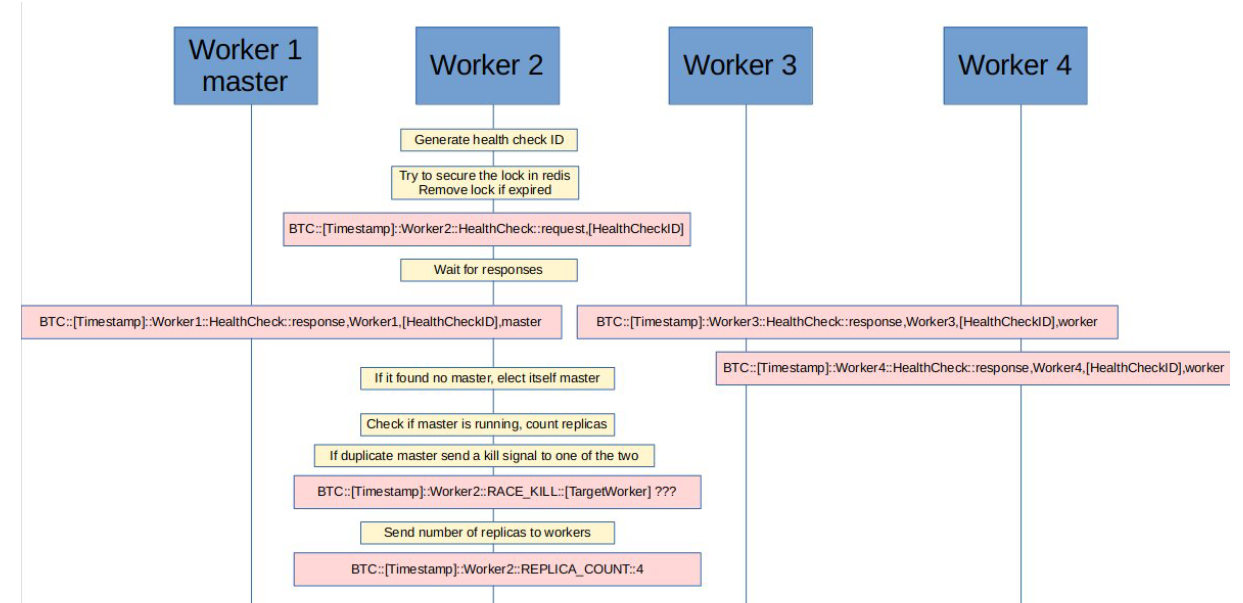
At some point, I came across a disturbing reality: as the distributed software would scale up for ingesting large bulks of historical data, the pressure on the messaging and health check locking mechanism would grow. The problem I needed to solve for optimal behaviour at any scale was then following: how often should my replicas health check, knowing how much siblings they have, for the probability of a race on the lock to be constant ?

Mathematical description of the problem

We want to dynamically give each replica a probability to trigger a health check at every time interval. We also want to choose the probability of two or more replicas health checking at the same time. We define the Binomial event $X$: "X replicas amongst $n$ have decided to health check in the time interval, each with a probability $p$ of occurence". We want to find $p$ such as $P(X\geq2)$ would have a probability to occur equal to $a$:

$$P(X \geq 2) = a$$

We then expand the formula to one ($X \geq 0$) minus its complementary ($X=0$ or $X=1$):

$$1 - P(X=0) - P(X=1) = a$$

And we substitute the binomial formula in it:

$$1 - (1-p)^{n-1} - (1 - p + np) = a$$

To find a solution to our equation, we now analyze the following function of $f: \mathbb{R} \rightarrow \mathbb{R}$, whose roots ($f(x)=0$) between 0 and 1 (it's a probability) will be solutions to our equation:

$$f(x) = 1 - a - (1-x)^{n-1}(1+(n-1)x)$$

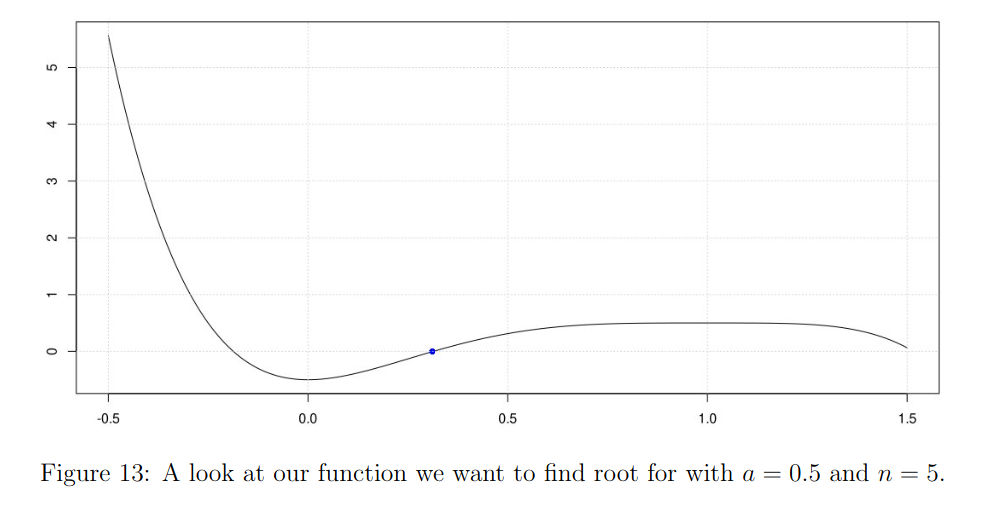
Computing a solution with Newton-Raphson method

I searched hard for a calculus based solution back in the days, and found none.

While this function may or may not be solved through calculus, I came to the realization that I could use analysis theorems and the Newton-Raphson method to approxiate a close enough solution inside the replicas. But could I ? That's what I now want to proove.

Derivatives and variation tables

We're going to look at this function's first and second order derivatives to see if there is room for a proof that the Newton-Raphson method converge to the root we want on some interval.

It's easy for anyone to see that this function can be derived if $n>1$, being a sum and a product of parts that can be derived. The first derivative is equal to:

$$f'(x)=(n-1)(1-x)^{n-2}xn$$

The second order derivative is now given by:

$$f''(x)=-(n-1)n(1-x)^{n-3}((n-1)x-2)$$

We pick a value $c<0$ in the neighbourhood of $0$ and $d>1$ in the neighbourhood of $1$, and look at the variation tables, first for $f(x)$:

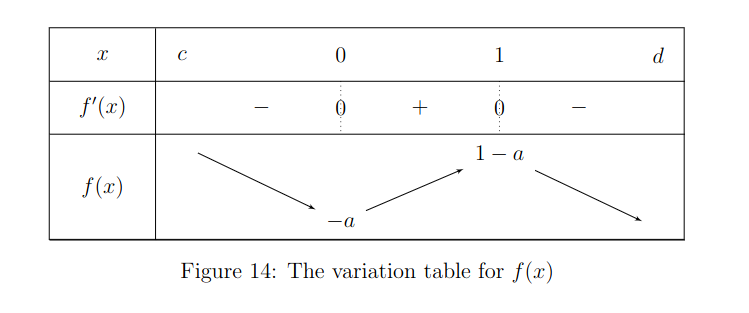
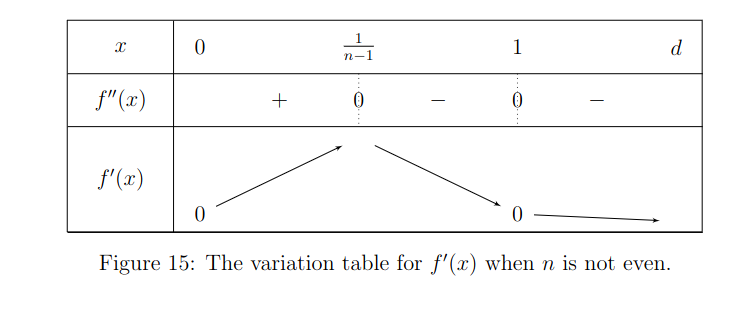
Then for the first and second order derivative, variation will depend on if $n$ is even or odd due to the exponents changing the sign. We have for $n$ not even:

And if it's even:

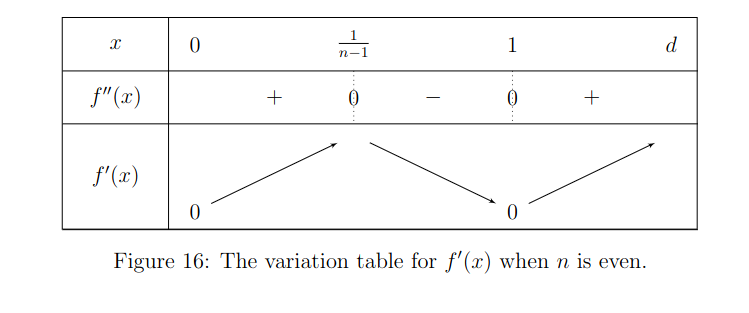
We observe two important things:

• By the intermediate value theorem, since $f(0)<0$ and $f(1)>0$, we know there exists $r \in ]0,1[$ such as $f(r)=0$.
• We also know given that the function $f$ between $0$ and $1$ is strictly monotonic that this $r$ is unique.

Proof that we always find the solution

So now we legitimally assume that there exists $r \in ]\frac{1}{n-1}, 1[$ such that $f(r)=0$. We then pick $a \in ]\frac{1}{n-1}, r[$ and $b$ such as $\forall \epsilon > 0,\; b = a + \epsilon,\; b\in]a,r[$.

Given that $\forall x \in ]\frac{1}{n-1}, 1[$, we have $f''(x)<0$ and $\forall x \in ]0, 1[$ there is $f'(x)>0$, we deduce that:

$$f'(a)>f'(b)$$

Then, knowing that we have $f(a)<f(b)$ and $a<b$ we also deduce that:

$$a-\frac{f(a)}{f'(a)} < b-\frac{f(b)}{f'(b)}$$

If we take $b=r$, this means that $a$ can't be greater than $r$ due to:

$$a-\frac{f(a)}{f'(a)} < r-\frac{f(r)}{f'(r)} = r$$

And if we now consider the Newton Raphon iteration formula where:

$$U_{n+1} = U_n - \frac{f(U_n)}{f'(U_n)}$$

We conclude that if $U_0 \in ]\frac{1}{n-1}, r[$, $U_n$ will be strictly growing and below $r$, and thus will tend to $r$! In this scenario, we have a solution to $f(x)=0$ and can find our perfect health check rate. The key to this proof is to make sure the sign of $f''(x)$ does not change on the interval we are running the interation on. A very similar proof can be used to proove that the method also applies if $r$ is below $\frac{1}{n-1}$. If $r=\frac{1}{n-1}$ the proof is trivial. I therefore can be sure that if I start in the right interval with the right value, ($\frac{1}{n-1}$ is a good one), I will always find the equation solution, and my probabilty of having two or more replicas racing in the interval will be equal to $a$.

Implementation in NodeJS

NodeJS is a good candidate for horizontally scaling and IO bound software, and this was my weapon of choice back when I made the distributed ETL. It may not be good for compting heavy duties, but it is not the case here as this method will converge geometrically (really fast). This was the implementation I ended up with back in the days:

// the upper and lower limit where binomial distrib function verify newton's method requirements
let minProbBinom = 0.15;
let maxProbBinom = 0.7;

// default to 12 healthchecks per minute in case of problems
let DEFAULT_HEALTHCHECK_CHANCE = 0.25;

// max newton method iteration number to consider it impossible
// should converge geometrically
let NEWTON_MAX_ITER = 2000;
// thresold for iteration differences after which we consider we converged
let NEWTON_ERR_THRESOLD = 0.001;


function findDistributedProtocolFreq(probability, replicas) {
    /*
     * compute the optimal distributed process rate per replica to have as much as probability parameter
     * chances of having two or more replicas health checking together in one step (most probably 1 second)
     * using the newton-raphson method to find root of an equation with the binomial distribution probability mass function P(X>=2)
     *
     * This implies we spawn the process as a bernouilli event of returned proba at each interval (or equivalent)
     * 
     * @returns rate per interval to maintain with required parameters
     */

    // if probability parameter is out of range, reply with default
    if(probability<0.00001 && probability>0.9995) {
        console.error("findDistributedProtocolFreq received out of range probability");
        // if it did, fallback to default
        return DEFAULT_HEALTHCHECK_CHANCE/replicas;
    }

    // if single replica, return the probability directly
    if(replicas==1) {
        return probability;
    }

    // define iteration function
    let fixedPointIteration = function (x) {
        // x_{p+1} = x_p - f(x)/f'(x)
        let fx = 1 - probability - ((1-x)**(replicas-1))*((1-x)+replicas*x);
        let fpx = (replicas-1)*x*replicas*((1-x)**(replicas-2));
        if(Number.isNaN( fx/fpx )==true) return x;
        return (x - (fx/fpx));
    };
    // now let's iterate to converge to the root
    let niter = 0;
    let sqerr = 1;
    let xn = 1/(replicas-1);
    // while we have not wasted too much trials or found satisfying result
    while(niter<NEWTON_MAX_ITER && sqerr>NEWTON_ERR_THRESOLD) {
        // compute next x
        let new_x = fixedPointIteration(xn);
        niter++;
        sqerr = Math.sqrt((xn-new_x)**2);
        xn = new_x;
    }
    // now we are done, check if it failed (shouldn't)
    if(niter>=NEWTON_MAX_ITER || xn<0 || xn>1) {
        // if it did, fallback to default
        return DEFAULT_HEALTHCHECK_CHANCE/replicas;
    }
    // if we have our probability of service occurence per second per replica
    // return it
    return xn;
}

module.exports = { findDistributedProtocolFreq };

Conclusion

We now know how to dynamically change the health check rate of all replicas so that the stress on the messaging and locking utilities does not increase with the number of replicas. The good thing is that in this specific protocol, I choosed a locking mechanism that was was fast but could fail at the cost of additional freeze time, and I perfectly control the probability of that occurence.

This solution to solve health check rates has been proven reliable, being in production for a few years already. The protocols are stable and no failure or scale related stress have been observed over the years, despite being sometimes scaled dramatically (1 to hundreds of replicas).

Spread the word

If you liked this article, feel free to share it on LinkedIn, send it to your friends, or review it. It really make it worth my time to have a larger audience, and it encourages me to share more tips and tricks. You are also welcome to report any error, share your feedback or drop a message to say hi!